Algorithms in JavaScript :-

Similarly to this first split, we can keep diving the array until we either find the element, or end up with only one candidate for the key.

Implementation of Binary Search in JavaScript

Now that we’ve gone through the logic behind Binary Search let us implement it in JavaScript:

function binarySearch(sortedArray, key){
let start = 0;
let end = sortedArray.length - 1;

while (start <= end) {
let middle = Math.floor((start + end) / 2);

if (sortedArray[middle] === key) {
// found the key
return middle;
} else if (sortedArray[middle] < key) {
// continue searching to the right
start = middle + 1;
} else {
// search searching to the left
end = middle – 1;
}
}
// key wasn’t found
return -1;
}

Big O Notation:-

Big O notation is just a way of representing the general growth in the computational difficulty of a task as you increase the data set. While there are other notations, O notation is generally the most used because it focuses on the worst-case scenario, which is easier to quantify and think about. Worst-case meaning where the most operations are needed to complete the task; if you solve a rubik’s cube in one second you can’t say you’re the best if it only took one turn to complete.

As you learn more about Big O notation, you’ll probably see many different, and better, variations of this graph. We want to keep our complexity as low and straight as possible, ideally avoiding anything above O(n).

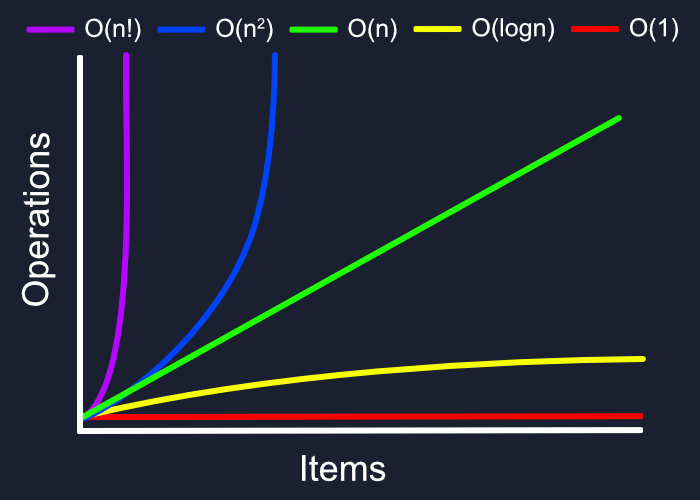
O(1)

This is the ideal, no matter how many items there are, whether one or one million, the amount of time to complete will remain the same. Most operations that perform a single operation are O(1). Pushing to an array, getting an item at a particular index, adding a child element, etc, will all take the same amount of time regardless of the array length.

class=”code-pre language-js”>const a1 = performance.now();
smArr.push(27);
const a2 = performance.now();
console.log(`Time: ${a2 - a1}`); // Less than 1 Millisecondconst b1 = performance.now();
bigArr.push(27);
const b2 = performance.now();
console.log(`Time: ${b2 – b1}`); // Less than 1 Millisecond

O(n)

By default, all loops are an example of linear growth because there is a one-to-one relationship between the data size and time to completion. So an array with 1,000 times more items will take exactly 1,000 times longer.

const a1 = performance.now();
smArr.forEach(item => console.log(item));
const a2 = performance.now();
console.log(`Time: ${a2 – a1}`); // 3 Milliseconds

const b1 = performance.now();
bigArr.forEach(item => console.log(item));
const b2 = performance.now();
console.log(`Time: ${b2 – b1}`); // 13 Milliseconds

O(n^2)

Exponential growth is a trap we’ve all fall into at least once. Need to find a matching pair for each item in an array? Putting a loop inside a loop is great way of turning an array of 1,000 items into a million operation search that’ll freeze your browser. It’s always better to have to do 2,000 operations over two separate loops than a million with two nested loops.

const a1 = performance.now();
smArr.forEach(() => {
arr2.forEach(item => console.log(item));
});
const a2 = performance.now();
console.log(`Time: ${a2 – a1}`); // 8 Milliseconds

const b1 = performance.now();
bigArr.forEach(() => {
arr2.forEach(item => console.log(item));
});
const b2 = performance.now();
console.log(`Time: ${b2 – b1}`); // 307 Milliseconds

O(log n)

The best analogy I’ve heard to understand logarithmic growth is to imagine looking up a word like ‘notation’ in a dictionary. You can’t search one entry after the other, instead you find the ‘N’ section, then maybe the ‘OPQ’ page, then search down the list alphabetically until you find a match.

With this ‘divide-and-conquer’ approach, the amount of time to find something will still change depending on the size of the dictionary but at nowhere near the rate of O(n). Because it searches in progressively more specific sections without looking at most of the data, a search through a thousand items may take less than 10 operations while a million may take less than 20, getting you the most bang for your buck.

In this example, we can do a simple quicksort.

const sort = arr => {
if (arr.length < 2) return arr;

let pivot = arr[0];
let left = [];
let right = [];

for (let i = 1, total = arr.length; i < total; i++) {
if (arr[i] < pivot) left.push(arr[i]);
else right.push(arr[i]);
};
return [
…sort(left),
pivot,
…sort(right)
];
};

sort(smArr); // 0 Milliseconds
sort(bigArr); // 1 Millisecond

O(n!)

Finally, one of the worst possibilities, factorial growth. The textbook example of this is the travelling salesman problem. If you have a bunch of cities of varying distance, how do you find the shortest possible route that goes between all of them and returns to the starting point? The brute force method would be to check the distance between every possible configuration between each city, which would be a factorial and quickly get out of hand.

Since that problem gets very complicated very quickly, we’ll demonstrate this complexity with a short recursive function. This function will multiply a number by its own function taking in itself minus one. Every digit in our factorial will run its own function until it reaches 0, with each recursive layer adding its product to our original number. So 3 is multiplied by 2 that runs the function to be multiplied by 1 that runs it again to be stopped at 0, returning 6. Recursion gets confusing like this pretty easily.

const factorial = n => {
let num = n;

if (n === 0) return 1
for (let i = 0; i < n; i++) {
num = n * factorial(n – 1);
};

return num;
};

factorial(1); // 2 Milliseconds
factorial(5); // 3 Milliseconds
factorial(10); // 85 Milliseconds
factorial(12); //  11,942 Milliseconds

Recursion:-

A base case is a condition that helps our recursive function stop. In our elevator example, it doesn’t continue going up past the top floor because there aren’t any more floors to pass. If you were looking in an array, the function shouldn’t go past the number of elements within it because then it’s not evaluating anything. An important thing to keep in mind when writing our base case is to make sure we use return to actually stop any code after it from running.

Combined with our base case, we need to make sure our input can actually reach our base case by ensuring that a different version of our input is used instead of the original. If we had a function called countDown that prints a count down and we input 10 and our base case is for it to stop once it hits 1, we need to make sure that when we call countDown with an 1 less than the previous input. That means that the next countDown input will be 9 and not 10. Otherwise, our function will never hit our base case.

Our recursive function’s basic layout might look like this:

function recursiveExample(input) {
Base Case:
If the input reaches this condition, return and stop the loop
Recursion:
Calls recursiveExample(altInput) with an altered input
}

Tail Recursion:-

When a recursive function uses tail recursion, it can be optimized by the JavaScript engine. This optimization is called Tail Call Optimization (TCO). The reason I say can is because Tail Call Optimization is part of the JavaScript language specification but it isn’t supported by very many browsers at the time of this writing.

Every time we call a function, a stack frame is created, which is a frame of data that stores information about that function call. This stack frame gets pushed onto the call stack, which is a stack data structure that stores all active function invocations.

When a recursive function has Tail Call Optimization, the call stack won’t continue to grow. To see this in action, visit the following two JSBin links in Safari with the Console open. Make sure your version of Safari is version 13 or higher.

• factorial(n) with TCO
• factorial(n) without TCO

factorial(n) With Tail Recursion:-

Here is the implementation with tail recursion: